先取り中3数学・「式と計算」に苦戦する理由を考えてみた
中2の12月は定期テストがないので、中3の数学の先取りに取り掛かることにしました。
そこで久しぶりに数学の難しさに直面しました。はじめはTry Itの動画授業に任せようと思っていたのですが、進度が早い !すぐに教科書ペースに切り替えましたが、教科書の進度も早い!数学が苦手な子は予習なしでは授業についていけないのではないかと思いました。
演習に基本が少なくすぐに応用問題がでてきます。教科書は入試のダイジェスト版なのか?と思うくらい。昔の教科書は基本をしっかりさせていた気がするのですが…教科書でも差はあるようです。啓林館は特にスピードが速いように感じます。はじめは啓林館のものを使用していましたが、数研出版に切り替えました。
文字式が一番難しい?
中3始めの単元は「式の計算」です。一番やりやすい単元です。…だと思っていました。しかしよつばには文字式が一番難しいようなのです。イメージがしづらいからなのかな、と思います。
よつばの場合、実例がベースとなる「場合の数」には苦労しませんでした。しかし「式の計算」ではスムーズにいきません。文字式に出てくる文字は実際の数を単純化したものです。その単純化がどうもしっくりこないようなのです。
数学ができないとは
- 理論を理解できない
- 公式を覚えられない
の大きく二本柱で成り立っています。どちらか一方ができればなんとかやっていけます。理論が理解できなくても公式が覚えられれはなんとかなります。公式が覚えられなくても理論から公式を導くことができます。
現実的には、理論を理解できないと応用できないし、公式が覚えられなければ時間が足りなくなるのでテストでは通用しません。どちらも大切です。
よつばにとってこの二点のどちらもが難しいのが「式と計算」なのです。
なぜ理論を理解できないのか?
「証明」が信用できない?
ネットで「数学苦手」で検索していると、苦手な子の驚くべき意見がありました。
「数学の公式がなぜそうなるか気になる。理解できない公式を使って計算するのは嫌だ。公式の意味を考えてしまうから私は数学ができないのだ」
としっかりと自己分析できているのは素晴らしいのですが、そのような意見は不思議でたまりませんでした。
数学の公式は教科書に証明が出ています。なのになぜ、公式が理解できないのか?
ずっと疑問でした。が、よつばが数学につまづく姿をみてやっと理解できました。どうやら教科書の証明を信じていなようなのです。
数学の証明は文字式で行われます。実際の数字をaやらXに置き換えます。数学が得意な子にとっては文字での置き換えは実例の単純化だと理解しており、すんなりと頭に入ります。しかし、その単純化が実感できないもの=得たいもの知れないものに感じる子もいます。実例でないと実感できないのです。
よつばには実例で成り立っているの「場合の数」や「図形の証明」は理解しやすかったようです。
公式が覚えられない?
中学数学の公式は大した量はありません。しかし、一定数、公式の暗記が苦手な子がいるようなのです。
え、公式が覚えられない?ヘロンの公式とか?
いえいえ、教科書レベルの公式をです。
よつばの場合、円柱や円錐、扇形の面積の公式はなんの問題もなく覚えていました。しかし文字式の公式は覚えづらいようです。文字がゴチャゴチャしている、と覚えづらいのでしょうか。理論の理解が浅いということもあるでしょうが、とにかく解いている最中は理論を思い出す余裕もないようなのです。
どうすれば公式を覚えるのかということに結論は出せません。しかし、以下のことに徹することにしました。
- 理論の理解が先
- 公式を忘れたら、基本理論に戻って公式を導かせる
- 焦らない、焦らせない
思い起こせば中1の「正の数、負の数」でも計算法をなかなか覚えられず苦労しました。しかし、なんとかマスターしました。とにかく焦らせずにしっかり理論を理解させることが一番だと思います。以下実践をつづってみました。
数学苦手「文字と式」の教え方
中3の「式の計算」では公式がたくさんでてきます。
- $$(a+b)(c+d)=ac+ad+bc+bd$$
- $$(x+a)(x+b)=x^2+(a+b)x+ab$$
- $$(x+a)^2=x^2+2ax+a^2$$
- $$(x-a)^2=x^2-2ax+a^2$$
- $$(x+a)(x-a)=x^2-a^2$$
1は中1レベルの分配の法則です。まずは分配の法則が理解できているかを確認することが大切です。
よつばの場合は、分配の法則は覚えておりました。よって2の式はスムーズに進みました。しかし、2~3の公式はスムーズにはいきませんでした。心づもりはしていましたので、焦らずゆっくり
- 公式は教える前に、自分で発見できるように導く。
- 公式を忘れたら、再度公式を導かせる
に徹することにしました。
公式は教える前に、自分で発見できるように導く。
例えば
3の公式 \((x+a)^2=x^2+2ax+a^2\)
は1の公式でも2の公式でも解くことができます。まずそれに気づかせるために以下の問題を1の公式で解かせます。(3の公式はまだ教えません。)
$$(x+1)^2$$
$$(x+2)^2$$
$$(x+3)^2$$
$$(x+4)^2$$
$$(x+5)^2$$
…
1 の公式で解くと
$$\begin{eqnarray} (x+1)^2&=&(x+1)(x+1)\\ &=&x^2+x+x+1\\ &=& x^2+2x+1\\ \end{eqnarray}$$
1の公式を使っているうちにある法則に気づきます。
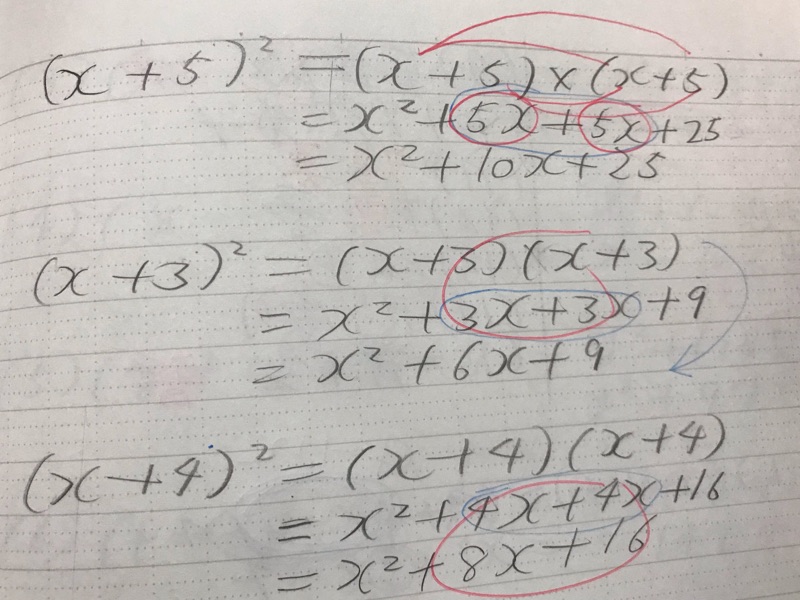
母:なんか気づいた?
よつば:うん、途中式に同じ数が出てくるね。
母:そう、2倍になっているでしょ。で、この公式ができました。じゃーん
$$(x+a)^2=x^2+2ax+a^2$$
同様に
$$(x-1)^2$$
$$(x-2)^2$$
$$(x-3)^2$$
…
は、
$$\begin{eqnarray} (x-1)^2&=&(x-1)(x-1)\\ &=&x^2-x-x+1\\ &=& x^2-2x+1\\ \end{eqnarray}$$
$$\begin{eqnarray} (x-2)^2&=&(x-2)(x-2)\\ &=&x^2-2x-2x+4\\ &=& x^2-4x+4\\ \end{eqnarray}$$
$$\begin{eqnarray} (x-3)^2&=&(x-3)(x-3)\\ &=&x^2-3x-3x+9\\ &=& x^2-6x+9\\ \end{eqnarray}$$
という式から公式を導かせます。よつばにとってはaという文字こそが理解を妨げているのでこのaを数値に置き換えるだけでぐっと分かりやすくなります。
もちろん、教科書でも実生活に身近になるように工夫されています。文字式の証明は面積を例として掲載されています。しかし、面積に例えられると式から想像しづらい気がします…
公式を忘れたら、再度公式を導かせる
公式を忘れたら、公式を使わずに計算させます。例えば公式2を忘れたなら公式1で、公式3、4、5を忘れたら公式2か1で計算させることで公式を導き出させます。
よつば:$$(x+4)^2=$$
あれ、なんだっけ?
母:公式を忘れたなら、まずは、分配の法則でやってごらん。
よつば:うん。
$$\begin{eqnarray} (x+4)^2&=&(x+4)(x+4)\\ &=&x^2+4x+4x+4^2\\ &=&x^2+8x+16\\ \end{eqnarray}$$
母:公式思い出した?
よつば:…
母:真ん中の\(4x\)は2回出てくるよね。
よつば:あ、\(2\)をかけるんだったね。
母:そう、公式は中間を省いただけだよ。じゃ、次は公式を使ってやってみて。
よつば:\((x+4)^2=x^2+2×4×x+4^2\)
この「式と計算」の分野はどの公式を使ってよいのかも悩む子もいます。しかし、公式の理解がしっかりしていれば大丈夫です。よつばもどのタイプにどの公式を適用できるかの判別は問題ありませんでした。
しかし、日が経つと忘れちゃうんですよね…。そうなるとまた上記のやりとりを繰り返します。まだまだ試行錯誤は続きそうです💦
以上でした。